Hendrick Matheus: abril 2014

segunda-feira, 21 de abril de 2014

Yin-yang

O exercício da aula, foi criar a função mostraYinYang(x, y, r), que desenha o símbolo do Yin-yang recebendo como parâmetros um ponto central (x, y) e o raio do círculo maior.

void setup(){
  size(400,400);
  background(200);
  noStroke();
}

void draw(){
  background(200);
  mostraYinYang(200,200,150);
}

void mostraYinYang(float x, float y, float r ){
 //metade  círculo inferior 
 fill(255);
 arc(x, y, 2 * r, 2 * r, 0, PI, PIE);
  
 //metade  círculo superior
 fill(0);
 arc(x, y, 2 * r, 2* r, PI, 2*PI, PIE);
  
 //circulos lado direito
 fill(0);
 ellipse(x + r/2, y, r, r); //circulo maior
 fill(255);
 ellipse(x + r/2, y, r/2.5, r/2.5); //circulo menor
 
// //círculos lado esquerdo
 fill(255);
 ellipse(x - r/2, y, r, r); //circulo maior
 fill(0);
 ellipse(x - r/2, y, r/2.5, r/2.5); //círculo menor
}

quinta-feira, 10 de abril de 2014

O harmonógrafo é um aparelho mecânico que através do movimento de pêndulos usa uma caneta para desenhar formas geométricas(bastante complexas em alguns exemplos) em uma superfície. A sua invenção data da metade do século XIX e teve certa popularidade até o início do século XX. Não existe certeza em relação a quem o inventou, mas o Professor de Matemática Hugh Blackburn, é comumente creditado como inventor oficial.

Funcionamento

O funcionamento do Harmógrafo é baseado em um conjunto de pêndulos que acionam uma caneta, que registra no papel o movimento resultante do sistema. Dependendo da frequência, amplitude e fase em que os pêndulos se movem, diferentes combinações de padrões aparecem no papel.

A freqüência dos pêndulo é controlada pelo comprimento da sua haste, a amplitude varia de acordo com a altura em que o pêndulo é lançado e diminui gradativamente ao longo do tempo em função do atrito de seus componentes e da caneta sobre o papel. A fase entre os pêndulos é determinada pelo momento relativo em que cada um é lançado.

Harmonograph from Antony Hall on Vimeo.

Tipos de Harmonógrafos

O Harmonógrafo Lateral usa dois pêndulos para controlar o movimento da caneta em relação ao papel. Um pêndulo move a caneta para frente e para trás em um eixo, e outro pêndulo move o papel em um eixo perpendicular.

Existem outros tipos de harmonografo com mais pêndulos, como exemplo abaixo que possui três. Neste caso dois pêndulos trabalham perpendicularmente movimentando a caneta e mais um terceiro pêndulo livre, que pode oscilar em qualquer direção, movimenta o papel.

Modelo Matemático

O Harmonógrafo cria as figuras usando os movimentos dos pêndulos amortecidos. Este movimento é descrito pela equação abaixo:

$x(t) = A \sin (tf + p) e^{-dt}, \,\!$

A é amplitude, t representa o tempo, f é a frequência, p é a fase, e d representa o amortecimento.

Já que o pêndulo pode mover-se sobre dois eixos de uma forma elíptica, devido ao princípio de sobreposição, o movimento da haste ligada à parte inferior do pêndulo ao longo de um eixo será descrito pela equação:

$x (t) = A_1 \ sin (tf_1 + p_1) e ^ {-d_1t} + A_2 \ sin (tf_2 + p_2) e ^ {-d_2t}. \, \!$

Uma vez que o movimento da caneta é composto pelos movimentos de dois pêndulos, se repete o mesmo princípio para o pêndulo no eixo Y. Dessa forma a trajetória em um harmonógrafo pode ser descrita pelas equações abaixo:

$x (t) = A_1 \ sin (tf_1 + p_1) e ^ {-d_1t} + A_2 pecado (tf_2 + p_2) e \ ^ {-d_2t}, \, \!$

$y (t) = A_3 \ sin (tf_3 + p_3) e ^ {-d_3t} + A_4 \ sin (tf_4 + P_4) e ^ {-d_4t}. \, \!$

Modelo Computacional

A principio foi um tanto complicado adaptar o modelo matemático já apresentado, ao Processing, as primeiras tentativas geraram figuras bastantes deformadas como a imagem abaixo, acredito que em grande parte devido a

dificuldade de encontrar os valores que criassem as formas desejadas:

Após algum tempo sem conseguir muito avanço, resolvi procurar algum exemplo na Internet que pudesse ajudar a solucionar o problema. Durante a pesquisa encontrei um código em JavaScript, que utilizava praticamente o mesmo modelo que eu estava tentando adaptar, e também um outro site que apresentava valores para os parâmetros das equações para gerar figuras específicas.

Depois de transcrever trechos do JavaScript para o Processing e utilizar os valores que encontrei, acredito que alcancei objetivos mais próximos ao do trabalho proposto, abaixo está o código do programa.

float A1 = 100, freq1 = 2, fase1 = 1/16, d1 = 0.02; 
float A2 = 100, freq2 = 2, fase2 = 3 / 2, d2 = 0.0315;
float A3 = 100, freq3 = 2, fase3 = 13 / 15, d3 = 0.02;
float A4 = 100, freq4 = 2, fase4 = 1, d4 = 0.02;
  
boolean novoHarmon = true;

void setup(){

  size(400,400);
  noStroke();
  background(255);

}
void draw(){
  
   if(novoHarmon)
      harmonografo(4);
}


void harmonografo(int image) {
   
   //algumas variações de valores que
   //geram diferentes imagens
   switch(image){
     
   case 1:
   //Imagem 1
   freq1=3.001; freq2=2; freq3=3 ;freq4=2; 
   d1=0.004; d2=0.0065; d3=0.008; d4=0.019; 
   fase1=0; fase2=0; fase3=PI/2; fase4=3*PI/2;
   break;
   
   case 2:
   //Imagem 2
   freq1=10; freq2=3; freq3=1; freq4=2; 
   d1=0.039; d2=0.006; d3=0; d4=0.0045;
   fase1=0; fase2=0; fase3=PI/2; fase4=0;
   break;   
   
   case 3:
   //Imagem 3
   freq1=2; freq2=6; freq3=1.002; freq4=3;
   d1=0.02; d2=0.0315; d3=0.02; d4=0.02;
   fase1=PI/16; fase2=3*PI/2; fase3=13 *PI/16; fase4=PI;
   break;
   
   case 4:
   //Imagem 4
   freq1=2.01; freq2=3; freq3=3; freq4=2;
   d1=0.0085; d2=0; d3=0.065; d4=0;
   fase1=0; fase2=7*PI/16; fase3=0; fase4=0;
   break;
   
   
   case 5:
   //Imagem Aleatória
   freq1 = (freq1 + random(0,10) / 40)%40;
   freq2 = (freq2 + random(0,10)/40) %40;
   freq3 = (freq3 + random(0,10) / 40)%40;
   freq4 = (freq4 + random(0,10) / 40)%40;
   fase1 += 0.05 % (PI*2);

   break;
   
   
   }
 
   for (float t = 0; t < 50; t+=0.001) {
       float posX =200 + A1 * sin(freq1 * t +  fase1) * exp(-d1 * t) + A2 * sin(freq2 * t +  fase2) * exp(-d2 * t);
       float posY =200 + A3 * sin(freq3 * t +  fase3) * exp(-d3 * t) + A4 * sin(freq4 * t +  fase4) * exp(-d4 * t);
       fill(0);
       ellipse(posX, posY , 1 ,1);
   }
        
   novoHarmon = false;
}

Versão com tempo variando a cada chamada da função draw:
https://www.dropbox.com/s/fmu3m5pmknjhltd/harmonographv2.rar

Seguem algumas imagens geradas pelo código acima:

Referências

1) http://en.wikipedia.org/wiki/Harmonograph

2)http://hernan.amiune.com/labs/harmonograph/animated-harmonograph.html

3)http://www.walkingrandomly.com/?p=151

4)http://www.ouvirativo.com.br/?p=763

terça-feira, 8 de abril de 2014

Crônometro

Ainda utilizando Coordenas Polares, a tarefa era implementar um crônometro. Para isso, usei a funçao millis() para contar o tempo, e a cada segundo o ângulo do ponteiro é decrementado em 6°.

int relogio;
int intervalo=1000;
float angulo = 90;
float raio = 130;
float posX;
float posY;

void setup(){
  relogio=millis();
  size(400,400);
  background(255);
}

void draw(){
  if (millis() > relogio+intervalo){
    relogio=millis();
    cronometro();
    angulo-=6;
   
  }  
}

void cronometro(){
  
  posX = 200 + cos(radians(angulo)) * raio;
  posY = 200 - sin(radians(angulo)) * raio;
  println(angulo);
  
  ellipse(200, 200, 300, 300);
  line(200,200, posX, posY);
        
}

Polígono regulares com Coordenadas Polares

Nesta aula a atividade foi proposta foi fazer um algoritmo para desenhar um polígono regular centralizado na tela com quantidade de lados informada no próprio código.

//Declaração de Variáveis
  int lados = 5;
  float raio = 100;
  float angulo = 45;
  
  float x[] = new float[lados+1];
  float y[] = new float[lados+1];

void setup(){
size(400,400);
background(255);
strokeWeight(1);

}
    
void draw(){
  background(255);
  
  //desenhar Grade
  line(0,height/2,width,height/2);
  line(width/2, 0 , width/2, height);
  
  //loop responsável por preencher os vetores 
  //que armazenam os pontos X e Y que formaram o polígono
  for(int circunf = 0;circunf < lados; circunf +=1){
        
        //cálculo do ponto X com o uso de coordenadas polares
        //posição x = raio * cos(angulo)    
        x[circunf] = 200 + cos(radians(angulo))*raio; 
        //cálculo do ponto Y com o uso de coordenadas polares
        //posição Y = raio * sen(angulo)  
        y[circunf] = 200 - sin(radians(angulo))*raio;
 
        // o valor do ângulo é calculado em função
        //do número de lados
        angulo += 360/lados;
 }
 //a última posição do vetor, recebe o primeiro
 //valor novamente, já que esse valor se repete
 //na formação da última linha
 x[lados]=x[0];
 y[lados]=y[0];
 
 //loop que monta o polígono utilizando os valores
 //armazenados anteriormente
 for(int i = 0; i<lados; i+=1){
    line(x[i],y[i] , x[i+1], y[i+1]);  
 }
 
 
}

Lançamento Oblíquo

Em um lançamento oblíquo o móvel se deslocará para a frente em uma trajetória que vai até uma altura máxima e depois volta a descer, formando uma trajetória parabólica.

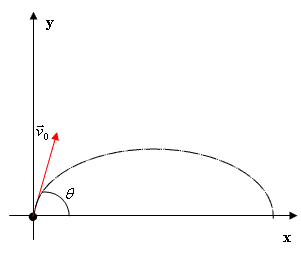
Para analisar o lançamento oblíquo é necessário considerá-lo como resultante de outros dois movimentos, um MRU na Horizontal e um MRUV na Vertical.

Na simulação realizada são fornecidos dois valores, o ângulo e velocidade inicial . Através destes valores é possível calcular a velocidade inicial dos dois movimento, que pode ser encontrada através das equações abaixo:

v0X = v0 * cos(angulo) e v0Y = v0 * sin(angulo);

Abaixo está o código implementado:

int relogio;
int intervalo=100;


//Váriaveis do Projétil
float dVert =height-1;
float dHoriz =1;

float angulo = 60;

float v0 = 100;
float v0X;
float v0Y;

float t = 0;
float a = -9.8;


//Variáveis do Alvo
float posXRect = 420;
float posYRect = 310;
float largRect = 50;
float altRect = 50;

void setup(){
  relogio=millis();
  size(700,700);
  
  //Cálculo da velocidade inicial nas direções
  //horizontal e vertical
  v0X = cos(radians(angulo)) * v0;
  v0Y = sin(radians(angulo)) * v0;

}

void draw(){

  if (millis() > relogio+intervalo){
    relogio=millis();

    lancBalist();
    t=t+0.1;
  }    
  
}

void lancBalist(){
    dHoriz = v0X * t;  //deslocamento horizontal(MRU)
    dVert = (v0Y * t) + a*(t*t)/2;//deslocamento Vertical(MRUV)
     
    background(255);
    desenhaGrade();
    mostraInfo();
    ellipse(dHoriz, height-dVert, 25, 25);
    
    
    //teste colisão sentido horizontal
    if((dHoriz+12.5 >= posXRect) && (dHoriz-12.5<=posXRect+largRect)){
        //teste colisão sentido vertical
        if((height-dVert >= posYRect) && (height-dVert<=posYRect + altRect) ){
        text("Colidiu",320, 310);

        fill(255, 0, 0);

        }
    }
}


void desenhaGrade(){
  for(int i = 0; i<=width; i+=100){
    text(height-i,0, i-5);
    text(i,i+5, height); 
    line(i, 0, i, height);
    line(0, i, width, i);
  }
  rect(posXRect, posYRect , largRect, altRect);
}

void mostraInfo(){
  textSize(10);
  fill(0);
  text("Deslocamento Vertical:" + dVert  +
       "\nDeslocamento Horizontal: "+ dHoriz+
       "\nVelocidade Vertical:" + (v0Y + a * t) +
       "\nVelocidade Horizontal: "+ v0X +
       "\nTempo: "+ t , width/2+10,20); 
}

Função meuRect

A tarefa dessa aula foi criar uma funçao que usando linhas e recebendo como parâmetros, centro, largura e altura desenhasse um quadrilátero.

void setup (){
  size(400, 400);
  background(255);
}

void draw (){
  
  meuRect(200,200,190,190);

}

void meuRect(int x, int y, int larg, int alt){
  
  int l = larg/2;
  int a = alt/2;
  
  line(x-l, y-a, x+l, y-a);
  line(x+l, y-a, x+l, y+a);
  line(x+l, y+a, x-l, y+a);
  line(x-l, y+a, x-l, y-a);
}

Hendrick Matheus

Páginas